Description

组合数 $\binom{n}{m}$ 表示的是从 $n$ 个物品中选出 $m$ 个物品的方案数。举个例子，从 $(1,2,3)$ 三个物品中选择两个物品可以有 $(1,2),(1,3),(2,3)$ 这三种选择方法。根据组合数的定义，我们可以给出计算组合数 $\binom{n}{m}$ 的一般公式：

$\binom{n}{m}=\frac{n!}{m!(n-m)!}$

其中 $n!=1\times2\times\cdots\times n$；特别地，定义 $0!=1$。

小葱想知道如果给定 $n,m$ 和 $k$，对于所有的 $0\leq i\leq n,0\leq j\leq \min \left ( i, m \right )$ 有多少对 $(i,j)$ 满足 $k|\binom{i}{j}$。

Input Format

第一行有两个整数 $t,k$，其中 $t$ 代表该测试点总共有多少组测试数据，$k$ 的意义见问题描述。

接下来 $t$ 行每行两个整数 $n,m$，其中 $n,m$ 的意义见问题描述。

Output Format

共 $t$ 行，每行一个整数代表所有的 $0\leq i\leq n,0\leq j\leq \min \left ( i, m \right )$ 中有多少对 $(i,j)$  满足 $k|\binom{i}{j}$。

1 2
3 3

1

2 5
4 5
6 7

0
7

Hint

【样例1说明】 在所有可能的情况中，只有 $\binom{2}{1} = 2$ 一种情况是 $2$ 的倍数。 【子任务】

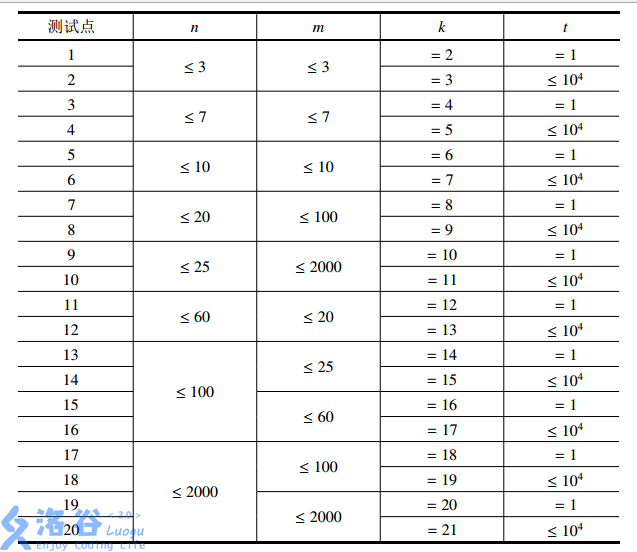
• 对于全部的测试点，保证 $0 \leq n, m \leq 2 \times 10^3$，$1 \leq t \leq 10^4$。